Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124
Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124
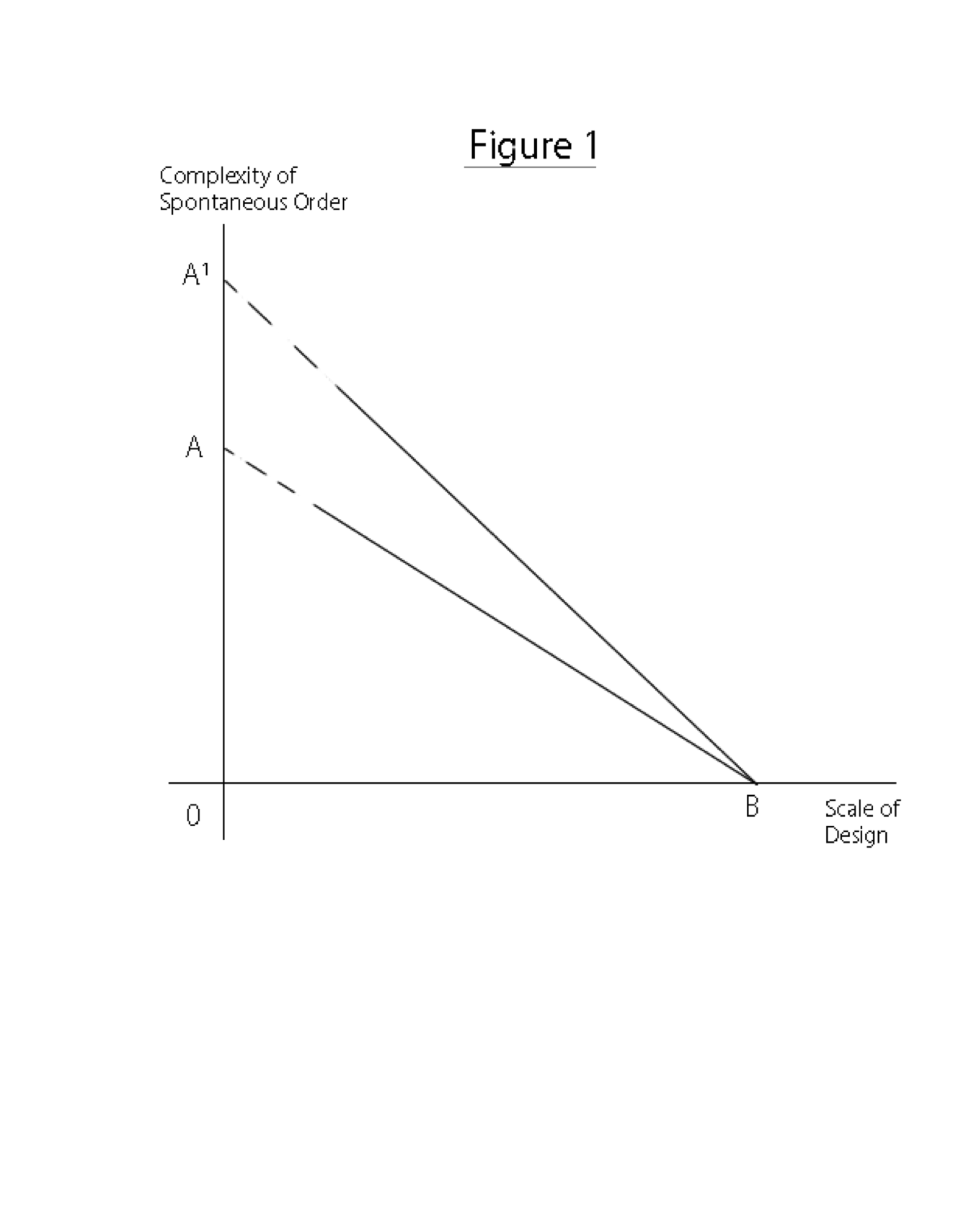
We can visualize the tradeoff between the scale of design and the complexity and spontaneity of a social order as a downward-sloping curve. A sort of “scale-versus-order-possibilities frontier.”
In addition to scale and spontaneous order/complexity, a third element I would add to the tradeoff is the passage of time. You can to some extent plan for complementarity, but you can’t really plan for spontaneous complexity and intricacy. [Helpful to bring in capital theory here?] Fortunately, time allows people to some extent to adjust social networks and physical spaces to better complement their own plans, in ways that the designer could not foresee. That is, for any given scale, time lets people figure out novel uses for, or changes to, the space as originally designed. Those unthought-of uses constitute an increase in the level of complexity in a spontaneous order. Over time, then, the frontier can shift outward.
Figure 1 reflects these relations:
The scale of a structure and the designed or planned uses of the space within that structure are of course two different things. Increasing the dimensions of a room doesn’t necessarily mean the elements that go into its design become more complex. But to keep things simple, Figure 1 treats scale and design as highly positively correlated. [Is this necessary?] Thus, as scale increases so do the designed elements – you move from point A to point B – and together they decrease the potential for spontaneous order. [But think about the tradeoff between scale and order, keeping design constant. Just increasing scale does seem to increase the designed/planned element in a previously undesigned space.]
Then, as time passes, the frontier shifts up from AB to A’B, where point B represents the case where the structure occupies100% of the relevant action space. So for any given scale, the passage of time allows people to find new, unplanned ways to interact with others in that space, thereby increasing the level of spontaneous order. How far it might shift in a given time period and the particular shape the tradeoff might take are critical issues, but unfortunately they are beyond what I can discuss here.
But thinking of the relation between scale, order, and time in this way can still help to explain how, despite the monumental scale of ancient Rome or Haussmann’s Paris or Niemeyer’s Brasilia or Ceausescu’s Bucharest, time has made those places more livable.
Now, what about the impact of deliberate design itself on spontaneous order?
Figure 2 isolates design from scale. It depicts a possible tradeoff between the potential for spontaneous order on the one hand, and the degree to which the order in the structure is planned rather than unplanned.
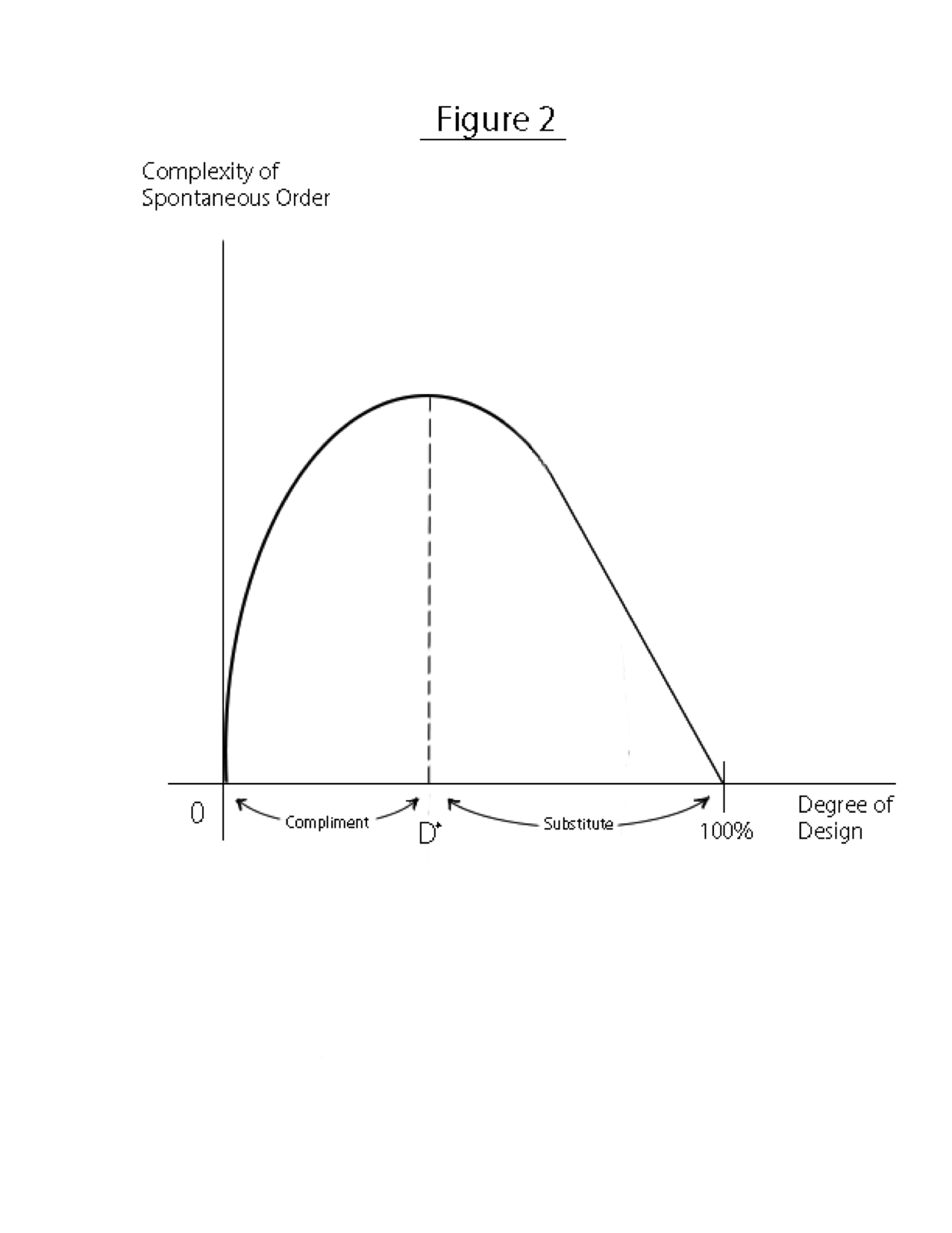
While I believe a space in which there is no deliberate, overall design can still give rise to spontaneous order, I have drawn the curve emanating from the origin – no overall design, no spontaneous order – but it rises steeply at first to reflect my own priors. [Elaborate on this; does this include rules or laws?] It then reaches a maximum level of potential spontaneous order at D*, beyond which design begins to substitute for rather than complement, unplanned order.
So, precisely because it is not a work of art, not the result of deliberate design, a city can achieve astonishing levels of intricacy, or of Jacobs’s “organized complexity.” But if not a work of art, then what is a city? I’ve been using the term “spontaneous order,” but what does it mean?
The City as a Spontaneous Order
Jacobs defines of a city as “a settlement that generates its own economic growth from its own local economy” (Jacobs 1969: 161). Ancient Rome and contemporary Washington, D.C. are not cities in this sense because on net they consume more wealth than they produce. While you could argue that each of these cities does create wealth, in the form of legislation and regulations that foster economic development, the consensus is that the output of legislation and regulation has for various reasons reached the point of negative returns. On the other hand, New York City is a city because, in addition to the net wealth it creates for the rest of the world, it generates more tax revenue for the rest of the country than it takes in in subsidies. In this sense, too, Paris, London, and Tokyo are also cities in Jacobs’s sense.
Note that Jacobs’s definition of a city is an economic one. It is different from, say, that of Richard Sennett: “…a city is a human settlement in which strangers are likely to meet” or of Edward Glaeser “At their core, cities are the absence of space between people and firms” both of which would include a prison, a mall, or Yankee Stadium.
[Add Weber, Pirenne here]
But it is a bit awkward to deny that Ancient Rome and contemporary Washington are cities. Perhaps Max Weber’s distinction between a “consumption city” and a “production city” might be more helpful. Instead, however, I have found it useful to term a “living city” what Jacobs defines as a city, and to use the term “city” to refer to any large settlement where strangers peacefully interact over a long time.
And as I am defining it here, a spontaneous order is a set of stable and coherent relations or patterns that is the result of human action but not of human design (Hayek 1967: 496). Moreover, it has the property of “emergence,” which is the ability of a complex system to arise from a multitude of individual interactions and to adapt to changing conditions without command. [Define “order” also?] It’s true that at some scale there is always deliberate design. Spontaneity exists at a level just above a set of designed elements. Thus the decision to buy from a particular supplier is deliberate, but the pattern of response of the entrepreneur over time to unexpected changes in supply (for example) is not. The architect’s plan of a home is designed, but how it interacts with other houses and those who live, work, and play in and around them over time to generate the character of a neighborhood is not. The spontaneity of an order then refers to the unplanned patterns that emerge over time at a level “above” a particular set of designed elements.
Like Jacobs, I see cities as highly adaptive systems that can achieve a level of complexity and orderly dynamism well beyond anything anyone could impose by design. Cities are the result of human action but, for the most part, not of human design. They are largely emergent, self-regulating, and self-sustaining.
I say “largely” of course because sometimes a city starts out as a deliberate creation and at different points in its history may be subject to extensive re-design. But over time, it evolves in ways that no one who played a part in its deliberate construction could have foreseen. The original designers of the New York City subway system in the late 19th century could not possibly have accurately predicted how the network would evolve over the next 100 years. And the ambitious public mega-projects undertaken at various points in a city’s history – such as Haussmann’s Paris – are eventually absorbed into the urban matrix. A city outgrows the elements designed at its beginnings or later in its history. The living flesh of a city heals, but no one can predict just how.
Like the spontaneous orders of language, judge-made law, and culture, cities evolve in response to myriad impulses from the people who constitute them. Cities thrive when there is freedom in one’s voluntary interactions with others. When they flourish, cities draw together socially distant strangers who are seeking profit, however they might interpret that word. And as Hayek explained in his essay of 1945, “The use of knowledge in society,” because people with limited knowledge can use the money prices that emerge from countless market exchanges as signals, the market process is much smarter than any human mind. In exactly the same way, the collective intelligence of a city can solve problems that no one can solve by herself. Even more importantly, cities serve to make us aware of what those problems are in the first place.
Now it’s true that some of these problems would not have existed but for large numbers of people with diverse knowledge, skills, and tastes packing themselves together into dense agglomerations. But these are also the conditions that foster informal contact. They make cities incubators of ideas and the principal sources cultural and scientific innovation.[1] Innovation and creativity are not possible without experimentation, trial-and-error; and trial-and-error is characteristically messy and often dangerous. Even though the number and diversity of opportunities you find in a city significantly lowers the uncertainty and the cost of experimenting, failure and disappointment will always be part of the bargain. Life on the cutting edge is the price and the value of living in a dynamic social order. Rem Koolhaas (1994: 59) put it well:
The entire spectacle defines the dark side of Metropolis as an astronomical increase in the potential for disaster only just exceeded by an equally astronomical increase in the ability to avert it. Manhattan is the outcome of that neck-and-neck race.
That, of course, could be said for any living city.
A city is the unintended consequence of people following their own plans, their own dreams. And when free to do so they will shape and abide by norms, conventions, beliefs, and institutions – i.e. the “rules of the game” – that promote social cooperation and create wealth in ways no one can fully imagine. And their choices will also intentionally or unintentionally nudge those norms, conventions, and the rest, in unpredictable directions. That is, as long as they are free to do so.
“Freedom” here means the ability to break old, strong ties and to make new, weak ties. All that making and breaking, like all change, entails some amount of disappointment, even tragedy. But the payoff, the “bright side of metropolis,” is creativity and innovation. In that sense, innovation and disappointment, creativity and conflict, go hand-in-hand. The same human tendencies that create the dark, destructive side of metropolis are responsible for the bright, creative side. Trying to eliminate the dark side, to put a stop to unwanted change, or imposing rules to avoid disappointment, stifles creativity, and results in even more profound disappointments. In other words, taxidermy. As long as ordinary people are free to apply their intelligence, knowledge, energy, and resourcefulness where they see the opportunity to do so, the forces of creation will stay just ahead of the gales of destruction. People will adjust to or change the built environment; more importantly, they will adjust to or change the invisible, social infrastructure.
But then amidst all this change and motion, how can we tell when things are getting better or worse?
[1] “The same age, which produces great philosophers and politicians, renown generals and poets, usually abounds with skilful weavers, and ship-carpenters.” David Hume
[In this space I’ll be posting quotes, ideas, and excerpts relating to a book I’m writing (thus far untitled), which I might describe as “What I have learned from the economic and social theory of Jane Jacobs.” My hope is to get thoughtful, informed feedback that will be useful in shaping the book.]